Axisymmetric cohesive element library

This section provides a reference to the axisymmetric cohesive elements available in Abaqus/Standard and Abaqus/Explicit.

Related Topics
About cohesive elements
Choosing a cohesive element
In Other Guides
*COHESIVE SECTION
Adhesive joints and bonded interfaces

ProductsAbaqus/StandardAbaqus/ExplicitAbaqus/CAE

Element types

General element

COHAX4

4-node axisymmetric cohesive element

Active degrees of freedom

1, 2 (ur, uz)

Additional solution variables

None.

Pore pressure element

COHAX4P(S)

6-node displacement and pore pressure axisymmetric cohesive element

CODAX4P(S)

6-node displacement and pore pressure axisymmetric cohesive element with the transition from Darcy flow to Poiseuille flow

Active degrees of freedom

1, 2, 8

Additional solution variables

None.

Nodal coordinates required

X,Y

Element property definition

You can define the element's initial constitutive thickness. The default initial constitutive thickness of cohesive elements depends on the response of these elements. For continuum response, the default initial constitutive thickness is computed based on the nodal coordinates. For traction-separation response, the default initial constitutive thickness is assumed to be 1.0. For response based on a uniaxial stress state, there is no default; you must indicate your choice of the method for computing the initial constitutive thickness. See Specifying the constitutive thickness for details.

Abaqus calculates the thickness direction automatically based on the midsurface of the element.

Input File Usage

COHESIVE SECTION

Abaqus/CAE Usage

Property module: Create Section: select Other as the section Category and Cohesive as the section Type

Element-based loading

Distributed loads

Distributed loads are specified as described in Distributed loads.

*dload
  1. Load ID (*DLOAD): BR
  2. Body force
  3. FL−3

  4. Body force in radial direction.

  1. Load ID (*DLOAD): BY
  2. Body force
  3. FL−3

  4. Body force in axial direction.

  1. Load ID (*DLOAD): BRNU
  2. Body force
  3. FL−3

  4. Nonuniform body force in radial direction with magnitude supplied via user subroutine DLOAD in Abaqus/Standard and VDLOAD in Abaqus/Explicit.

  1. Load ID (*DLOAD): BZNU
  2. Body force
  3. FL−3

  4. Nonuniform body force in axial direction with magnitude supplied via user subroutine DLOAD in Abaqus/Standard  and VDLOAD in Abaqus/Explicit.

  1. Load ID (*DLOAD): CENT(S)
  2. Not supported
  3. FL−4(ML−3T−2)

  4. Centrifugal load (magnitude is input as ρ⁢ω2, where ρ is the mass density per unit volume, ω is the angular velocity).

  1. Load ID (*DLOAD): CENTRIF(S)
  2. Rotational body force
  3. T−2

  4. Centrifugal load (magnitude is input as ω2, where ω is the angular velocity).

  1. Load ID (*DLOAD): GRAV
  2. Gravity
  3. LT−2

  4. Gravity loading in a specified direction (magnitude is input as acceleration).

  1. Load ID (*DLOAD): Pn
  2. Pressure
  3. FL−2

  4. Pressure on face n.

  1. Load ID (*DLOAD): PnNU
  2. Not supported
  3. FL−2

  4. Nonuniform pressure on face n with magnitude supplied via user subroutine DLOAD in Abaqus/Standard and VDLOAD in Abaqus/Explicit.

  1. Load ID (*DLOAD): SBF(E)
  2. Not supported
  3. FL−5T2

  4. Stagnation body force in radial and axial directions.

  1. Load ID (*DLOAD): SPn(E)
  2. Not supported
  3. FL−4T2

  4. Stagnation pressure on face n.

  1. Load ID (*DLOAD): VBF(E)
  2. Not supported
  3. FL−4T

  4. Viscous body force in radial and axial directions.

  1. Load ID (*DLOAD): VPn(E)
  2. Not supported
  3. FL−3T

  4. Viscous pressure on face n, applying a pressure proportional to the velocity normal to the face and opposing the motion.

Surface-based loading

Distributed loads

Surface-based distributed loads are specified as described in Distributed loads.

*dsload
  1. Load ID (*DSLOAD): P
  2. Pressure
  3. FL−2

  4. Pressure on the element surface.

  1. Load ID (*DSLOAD): PNU
  2. Pressure
  3. FL−2

  4. Nonuniform pressure on the element surface with magnitude supplied via user subroutine DLOAD in Abaqus/Standard  and VDLOAD in Abaqus/Explicit.

  1. Load ID (*DSLOAD): SP(E)
  2. Pressure
  3. FL−4T2

  4. Stagnation pressure on the element surface.

  1. Load ID (*DSLOAD): VP(E)
  2. Pressure
  3. FL−3T

  4. Viscous pressure applied on the element surface. The viscous pressure is proportional to the velocity normal to the element face and opposing the motion.

Element output

Stress, strain, and other tensor components available for output depend on whether the cohesive elements are used to model adhesive joints, gaskets, or delamination problems. You indicate the intended usage of the cohesive elements by choosing an appropriate response type when defining the section properties of these elements. The available response types are discussed in Defining the constitutive response of cohesive elements using a continuum approach and Defining the constitutive response of cohesive elements using a traction-separation description.

Cohesive elements using a continuum response

Stress and other tensors (including strain tensors) are available for elements with continuum response. Both the stress tensor and the strain tensor contain true values. For the constitutive calculations using a continuum response, only the direct through-thickness and the transverse shear strains are assumed to be nonzero. All the other strain components (i.e., the membrane strains) are assumed to be zero (see Modeling of an adhesive layer of finite thickness for details). All tensors have the same number of components. For example, the stress components are as follows:

S11

Direct membrane stress.

S22

Direct through-thickness stress.

S33

Direct membrane stress.

S12

Transverse shear stress.

Cohesive elements using a uniaxial stress state

Stress and other tensors (including strain tensors) are available for cohesive elements with uniaxial stress response. Both the stress tensor and the strain tensor contain true values. For the constitutive calculations using a uniaxial stress response, only the direct through-thickness stress is assumed to be nonzero. All the other stress components (i.e., the membrane and transverse shear stresses) are assumed to be zero (see Modeling of gaskets and/or small adhesive patches for details). All tensors have the same number of components. For example, the stress components are as follows:

S22

Direct through-thickness stress.

Cohesive elements using a traction-separation response

Stress and other tensors (including strain tensors) are available for elements with traction-separation response. Both the stress tensor and the strain tensor contain nominal values. The output variables E, LE, and NE all contain the nominal strain when the response of cohesive elements is defined in terms of traction versus separation. All tensors have the same number of components. For example, the stress components are as follows:

S22

Direct through-thickness stress.

S12

Transverse shear stress.

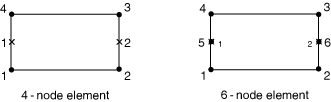
Node ordering and face numbering on elements



Table 1. Element faces
Face 1 1 – 2 face
Face 2 2 – 3 face
Face 3 3 – 4 face
Face 4 4 – 1 face

Numbering of integration points for output