Preprocessing—creating the model with Abaqus/CAE | ||
| ||
-
A Python script for this example is provided in Blast loading on a stiffened plate. Instructions on how to fetch the script and run it within Abaqus/CAE are given in Example Files.
-
A plug-in script for this example is available in the Abaqus/CAE Plug-in toolset. To run the script from Abaqus/CAE, select ; highlight Blast loading on a stiffened plate; and click . For more information about the Getting Started plug-ins, see Running the Getting Started with Abaqus examples.
- Defining the model geometry
-
Create a three-dimensional, deformable part with an extruded shell base feature to represent the plate. Use an approximate part size of 5.0, and name the part Plate. A suggested approach for creating the part geometry shown in Figure 1 is summarized in the following procedure:
Figure 1. Sketch of the stiffened plate (with grid spacing doubled).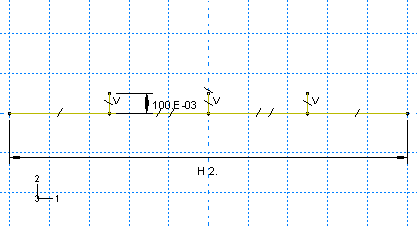
To create the stiffened plate geometry:
-
To define the plate geometry, use the Create Lines: Connected tool to sketch an arbitrary horizontal line.
-
To define the stiffener geometry, add three vertical lines extending up from the plate. The horizontal position of these lines is arbitrary at this stage, but their endpoints must snap to the horizontal line.
-
Constrain the three vertical lines so they are of equal length, and dimension one of them so that it is 0.1 m long.
-
Split the plate at the points where it intersects the stiffeners.
-
Dimension the horizontal distance between the plate endpoints, and set the value to 2.0 m.
-
Apply equal length constraints to the four horizontal segments of the line.
The final part sketch is shown in Figure 1.
-
Extrude the sketch to a depth of 2.0 m to create the plate.
-
- Defining the material properties
-
Define the material and section properties for the plate and the stiffeners.
Create a material named Steel with a mass density of 7800 kg/m3, a Young's modulus of 210.0E9 Pa, and a Poisson's ratio of 0.3. At this stage we do not know whether there will be any plastic deformation, but we know the value of the yield stress and the details of the post-yield behavior for this steel. We will include this information in the material definition. The initial yield stress is 300 MPa, and the yield stress increases to 400 MPa at a plastic strain of 35%. To define the plastic material properties, enter the yield stress and plastic strain data shown in Figure 1. The plasticity stress-strain curve is shown in Figure 2.
Figure 2. Yield stress versus plastic strain.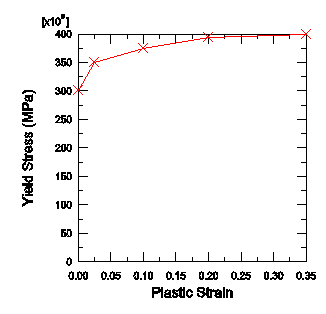
During the analysis Abaqus calculates values of yield stress from the current values of plastic strain. As discussed earlier, the process of lookup and interpolation is most efficient when the stress-strain data are at equally spaced values of plastic strain. To avoid having the user input regular data, Abaqus/Explicit automatically regularizes the data. In this case the data are regularized by Abaqus/Explicit by expanding the data to 15 equally spaced points with increments of 0.025.
To illustrate the error message that is produced when Abaqus/Explicit cannot regularize the material data, you could set the regularization tolerance to 0.001 (in the Edit Material dialog box, select ) and include one additional data pair, as shown in Table 1. You can add a row by clicking mouse button 3 in the table and selecting Insert Row from the menu that appears.
Table 1. Modified plasticity data. Yield Stress (Pa) Plastic Strain 300.0E6 0.000 349.0E6 0.001 350.0E6 0.025 375.0E6 0.100 394.0E6 0.200 400.0E6 0.350 The combination of the low tolerance value and the small interval in the user-defined data would lead to difficulty in regularizing this material definition. The following error message would be written to the status (.sta) file and displayed in the Job Monitor dialog box in the Job module:
***ERROR: Failed to regularize material data for material STEEL. Please check your input data to see if they meet both criteria as explained in "MATERIAL DATA DEFINITION" section of the Abaqus Materials Guide. In general, regularization is more difficult if the smallest interval defined by the user is small compared to the range of the independent variable.
Before continuing, set the regularization tolerance back to the default value (0.03) and remove the additional pair of data points.
- Creating and assigning section properties
-
Create two homogeneous shell section properties, each referring to the steel material definition but specifying different shell thicknesses. Name the first shell section property PlateSection, select Steel as the material, and specify 0.025 m as the value for the Shell thickness. Name the second shell section property StiffSection, select Steel as the material, and specify 0.0125 m as the value for the Shell thickness.
Assign the StiffSection definition to the stiffeners (use Shift to select multiple regions in the viewport).
Before assigning the PlateSection definition to the plate, consider the following. If the plate and the stiffeners are joined directly at their midsurfaces (this is the default behavior), an area of material overlap will occur, as shown in Figure 3.
Figure 3. Overlapping material.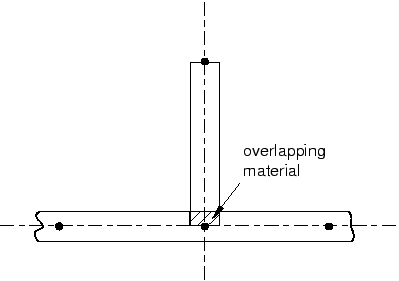
Although the thicknesses of the plate and stiffener are small in comparison to the overall dimensions of the structure (so that this overlapping material and the extra stiffness it creates would have little effect on the analysis results), a more precise model can be created by offsetting the plate reference surface from its midsurface. This technique allows the stiffeners to butt up against the plate without overlapping any material with the plate, as shown in Figure 4.
Figure 4. Stiffener joint in which the plate's reference surface is offset from its midsurface.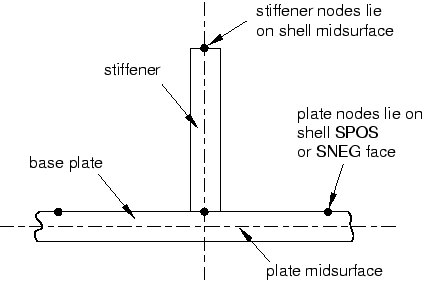
To determine whether to offset the plate reference surface to its positive (SPOS) or negative (SNEG) side, query the shell normals () and note the color of the side of the plate facing the stiffeners (brown is the positive side; purple is the negative side). If necessary, flip the plate normals () so that its segments have consistent normals. Then assign the PlateSection definition to the regions of the plate. In the Edit Section Assignment dialog box, set the shell offset to Top surface if the brown (positive) side of the plate faces the stiffeners and Bottom surface if the purple (negative) side faces the stiffeners.
To verify the offset, select . In the Part Display Options dialog box that appears, toggle on Render shell thickness. If necessary, modify the offset to remove any overlap.
The model can be color-coded according to section assignment to verify that properties were assigned correctly (select Sections from the Color Code toolbar).
- Creating an assembly
-
Create an independent instance of the plate. Use the default rectangular coordinate system, with the plate lying in the 1–3 plane.
At this point, it is convenient to create the geometry sets that will be used to specify boundary conditions and output requests. Create one set named Edge for the plate edges and one set named Center at the center of the intersection of the plate and the middle stiffener, as shown in Figure 5. To create the set Center, you need to first partition the edge of the original part in half using the Partition Edge: Enter Parameter
 tool.
Figure 5. Geometry sets.
tool.
Figure 5. Geometry sets.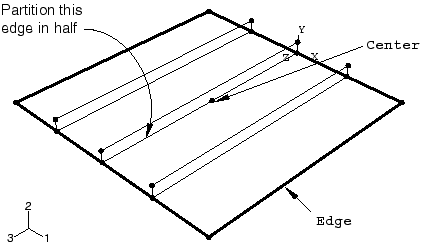
- Defining steps and output requests
-
Create a single dynamic, explicit step. Name the step Blast, and specify the following step description: Apply blast loading. Enter a value of 50E-3 s for the time period of the step.
In general, you should try to limit the number of frames written during the analysis to keep the size of the output database file reasonable. In this analysis saving information every 2 ms should provide sufficient detail to study the response of the structure. Edit the default output request F-Output-1, and set the number of intervals during the step at which preselected field data are saved to 25. This ensures that the selected data are written every 2 ms since the total time for the step is 50 ms.
A more detailed set of output for selected regions of the model can be saved as history output. Create a history output request named Center-U2 for the step Blast. Select Center as the output domain, and select U2 as the translation output variable. Enter 500 as the number of intervals at which the output will be saved during the analysis.
- Prescribing boundary conditions and loads
-
Next, define the boundary conditions used in this analysis. In the step Blast, create a Symmetry/Antisymmetry/Encastre mechanical boundary condition named Fix edges. Apply the boundary condition to the edges of the plate using the geometry set Edge, and specify ENCASTRE (U1 = U2 = U3 = UR1 = UR2 = UR3 = 0) to fully constrain the set.
The plate will be subjected to a load that varies with time: the pressure increases rapidly from zero at the start of the analysis to its maximum of 7.0 × 105 Pa in 1 ms, at which point it remains constant for 9 ms before dropping back to zero in another 10 ms. It then remains at zero for the remainder of the analysis. See Figure 6 for details.
Figure 6. Pressure load as a function of time.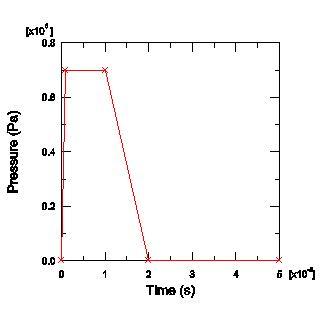
Define a tabular amplitude curve named Blast. Enter the amplitude data given in Table 2, and specify a smoothing parameter of 0.0.
Table 2. Blast load amplitude. Time Amplitude 0.0 0.0 1.0E−3 7.0E5 10.0E−3 7.0E5 20.0E−3 0.0 50.0E−3 0.0 Next, define the pressure loading. Since the magnitude of the load will be defined by the amplitude definition, you need to apply only a unit pressure to the plate. Apply the pressure so that it pushes against the top of the plate (where the stiffeners are on the bottom of the plate). Such a pressure load will place the outer fibers of the stiffeners in tension.
To define the pressure loading:
-
In the Model Tree, double-click the Loads container. In the Create Load dialog box that appears, name the load Pressure load and select Blast as the step in which it will be applied. Select Mechanical as the load category and Pressure as the load type. Click .
-
Select all the surfaces associated with the plate. When the appropriate surfaces are selected, click .
Abaqus/CAE uses two different colors to indicate the two sides of the shell surface. To complete the load definition, the colors must be consistent on each side of the plate.
-
If necessary, select in the prompt area to flip the colors for a region of the plate. Repeat this procedure until all of the faces on the top of the plate are the same color.
-
In the prompt area, select the color representing the side of the plate without the stiffeners.
-
In the Edit Load dialog box that appears, specify a uniform pressure of 1.0 Pa, and select the amplitude definition Blast. Click to complete the load definition.
The plate load and boundary conditions are shown in Figure 7.
Figure 7. Pressure load and boundary conditions.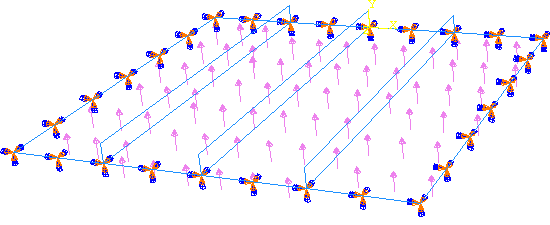
-
- Creating the mesh and defining a job
-
Seed the part instance with a global element size of 0.1. In addition, select and specify that two elements be created along the height of each stiffener (in the Local Seeds dialog box, select By number as the method and set the number of elements to 2; toggle on the option to create a set containing the selected edges). Mesh the plate and stiffeners using quadrilateral shell elements (S4R) from the Explicit element library. The resulting mesh is shown in Figure 8. This relatively coarse mesh provides moderate accuracy while keeping the solution time to a minimum.
Figure 8. Meshed plate.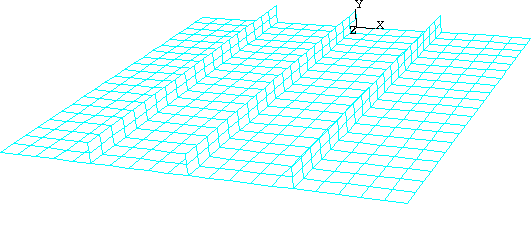
Create a job named BlastLoad. Specify the following job description: Blast load on a flat plate with stiffeners: S4R elements (20x20 mesh) Normal stiffeners (20x2).
Save your model in a model database file, and submit the job for analysis. Monitor the solution progress; correct any modeling errors that are detected, and investigate the cause of any warning messages.