Annealing or melting | ||||||||
|
| |||||||
ProductsAbaqus/StandardAbaqus/ExplicitAbaqus/CAE
Effects of annealing or melting
When the temperature of a material point exceeds a user-specified value called the annealing temperature, Abaqus assumes that the material point loses its hardening memory. The effect of prior work hardening is removed by setting the equivalent plastic strain to zero. For kinematic and combined hardening models the backstress tensor is also reset to zero. If the temperature of the material point falls below the annealing temperature at a subsequent point in time, the material point can work harden again. Depending on the temperature history a material point may lose and accumulate memory several times, which in the context of modeling melting would correspond to repeated melting and resolidification. Any accumulated material damage is not healed when the annealing temperature is reached. Damage will continue to accumulate after annealing according to any damage model in effect (see About damage and failure for ductile metals).
In Abaqus/Explicit an annealing step can be defined to simulate the annealing process for the entire model, independent of temperature; see Annealing for details.
![]()
Material properties
The annealing temperature is a material property that can optionally be defined as a function of field variables. This material property must be used in conjunction with an appropriate definition of material properties as functions of temperature for the Mises plasticity model. In particular, the hardening behavior must be defined as a function of temperature and zero hardening must be specified at or above the annealing temperature. In general, hardening receives contributions from two sources. The first source of hardening can be classified broadly as static, and its effect is measured by the rate of change of the yield stress with respect to the plastic strain at a fixed strain rate. The second source of hardening can be classified broadly as rate dependent, and its effect is measured by the rate of change of the yield stress with respect to the strain rate at a fixed plastic strain.
For the Mises plasticity model, if the material data that describe hardening (both static and rate-dependent contributions) are completely specified through tabular input of yield stress versus plastic strain at different values of the strain rate (see Rate-dependent yield), the (temperature-dependent) static part of the hardening at each strain rate is specified by defining several yield stress versus plastic strain curves (each at a different temperature). For metals the yield stress at a fixed strain rate typically decreases with increasing temperature. Abaqus expects the hardening at each strain rate to vanish at or above the annealing temperature and issues an error message if you specify otherwise in the material definition. Zero (static) hardening can be specified by simply specifying a single data point (at zero plastic strain) in the yield stress versus plastic strain curve at or above the annealing temperature. In addition, you must also ensure that at or above the annealing temperature, the yield stress does not vary with the strain rate. This can be accomplished by specifying the same value of yield stress at all values of strain rate in the single data point approach discussed above.
Alternatively, the static part of the hardening can be defined at zero strain rate, and the rate-dependent part can be defined utilizing the overstress power law (see Rate-dependent yield). In that case, zero static hardening at or above the annealing temperature can be specified by specifying a single data point (at zero plastic strain) in the yield stress versus plastic strain curve at or above the annealing temperature. The overstress power law parameters can also be appropriately selected to ensure that at or above the annealing temperature the yield stress does not vary with strain rate. This can be accomplished by selecting a large value for the parameter (relative to the static yield stress) and setting the parameter .
For hardening defined in Abaqus/Standard with user subroutine UHARD, Abaqus/Standard checks the hardening slope at or above the annealing temperature during the actual computations and issues an error message if appropriate.
The Johnson-Cook plasticity model in Abaqus/Explicit requires a separate melting temperature to define the hardening behavior. If the annealing temperature is defined to be less than the melting temperature specified for the metal plasticity model, the hardening memory is removed at the annealing temperature and the melting temperature is used strictly to define the hardening function. Otherwise, the hardening memory is removed automatically at the melting temperature.
Input File Usage
ANNEAL TEMPERATURE
Abaqus/CAE Usage
Property module: material editor: :
Example: Annealing or melting
The following input is an example of a typical usage of the annealing or melting capability. It is assumed that you have defined the static stress versus plastic strain behavior (see Figure 1) for the isotropic hardening model at three different temperatures, including the annealing temperature. It is also assumed that the plastic behavior is rate independent.
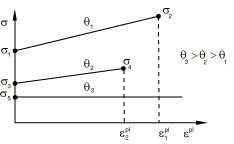
The plastic response corresponds to linear hardening below the annealing temperature and perfect plasticity at the annealing temperature. The elastic properties, which may also be temperature dependent, are not shown.
| Plasticity Data, Isotropic Hardening: | ||
|---|---|---|
| Yield Stress | Plastic Strain | Temperature |
| 0 | ||
| 0 | ||
| 0 | ||
| Anneal Temperature: | ||
![]()
Elements
This capability can be used with all elements that include mechanical behavior (elements that have displacement degrees of freedom).
![]()
Output
Only the equivalent plastic strain (output variable PEEQ) and the backstress (output variable ALPHA) are reset to zero at the melting temperature. The plastic strain tensor (output variable PE) is not reset to zero and provides a measure of the total plastic deformation during the analysis. In Abaqus/Standard the plastic strain tensor also provides a measure of the plastic strain magnitude (output variable PEMAG).