Shear flexible small-strain shell elements

This section discusses the formulation of the small-strain shear flexible elements in Abaqus/Standard, which are quadrilaterals (S4R5, S8R5, S9R5, and S8R), except for the 6-node triangle STRI65.

The following topics are discussed:

Notation
Surface measures
Displacements
Interpolation
Strains
Penalties
First variations of strain
Second variations of strains
Internal virtual work rate
Pressure load stiffness

Notation

A typical piece of shell surface is shown in Figure 1.

Figure 1. Shell reference surface.

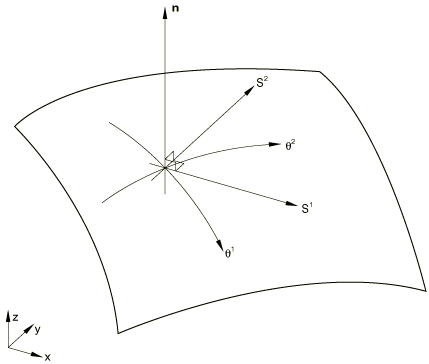
Let ( $θ^{1}$ , $θ^{2}$ ) be a set of Gaussian surface coordinates on the shell reference surface. Since these coordinates are only needed locally at an integration point, we use the element's isoparametric coordinates as these coordinates. $x (θ^{1}, θ^{2})$ is the current position of a point on the interpolated reference surface, and $X (θ^{1}, θ^{2})$ is the initial position of the same point. The unit vector

N = \frac{\partial X}{\partial θ^{1}} \times \frac{\partial X}{\partial θ^{2}} / \sqrt{\frac{\partial X}{\partial θ^{1}} \times \frac{\partial X}{\partial θ^{2}}}

is the unit normal to the interpolated reference surface in the initial configuration. This vector gives a “sidedness” to the surface—one surface of the shell is the “top” surface (in the positive direction along $N$ from the shell's reference surface) and the other is the bottom surface. The vector corresponding to $N$ in the current configuration, $n$ , will be made approximately normal to the reference surface in the current configuration by imposing the Kirchhoff constraint discretely.

In the rest of this section Greek indices will be used to indicate values associated with the (two-dimensional) reference surface and so will sum over the range 1, 2 under the summation convention.

First, we establish convenient directions for stress and strain output. These will be local material directions, indistinguishable (to the order of approximation) from corotational directions, since we assume strains are small. The standard convention used throughout Abaqus for such local directions on a surface is as follows.

It is most convenient to choose orthogonal directions. Define

T_{2} = \frac{N \times i}{\sqrt{N \times i}}

so long as $N_{1} < \cos {0.1}^{\circ}$ , where $i$ is a unit vector in the global X-direction; otherwise,

T_{2} = \frac{N \times k}{\sqrt{N \times k}},

where $k$ is a unit vector in the global Z-direction. Then define

T_{1} = T_{2} \times N .

Let

d S^{β} = T_{β} \cdot \frac{\partial X}{\partial θ^{α}} d θ^{α},

so that the $d S^{α}$ are locally defined distance measuring coordinates at each material point. The transformation

\frac{\partial}{\partial S^{α}} = \frac{\partial θ^{β}}{\partial S^{α}} \frac{\partial}{\partial θ^{β}}

transforms locally with respect to surface coordinates. Here

\frac{\partial θ^{α}}{\partial S^{β}} = {[\begin{matrix} T_{1} \cdot \partial X / \partial θ^{1} & T_{1} \cdot \partial X / \partial θ^{2} \\ T_{2} \cdot \partial X / \partial θ^{1} & T_{2} \cdot \partial X / \partial θ^{2} \end{matrix}]}^{- 1} .

Stress and strain components are formed in the ( $d S^{1}$ , $d S^{2}$ ) directions.

Surface measures

The following surface measures are defined. The metric of the deformed surface is

g_{α β} = \frac{\partial x}{\partial S^{α}} \cdot \frac{\partial x}{\partial S^{β}},

and an approximation to the curvature tensor (the second fundamental form) is

b_{α β} = - \frac{1}{2} (\frac{\partial n}{\partial S^{α}} \cdot \frac{\partial x}{\partial S^{β}} + \frac{\partial n}{\partial S^{β}} \cdot \frac{\partial x}{\partial S^{α}})

(this is only an approximation because $n$ is not exactly normal to the surface in the current configuration).

The corresponding measures associated with the original reference surface are the metric

G_{α β} = \frac{\partial X}{\partial S^{α}} \cdot \frac{\partial X}{\partial S^{β}}

and the approximation to the curvature

B_{α β} = - \frac{1}{2} (\frac{\partial N}{\partial S^{α}} \cdot \frac{\partial X}{\partial S^{β}} + \frac{\partial N}{\partial S^{β}} \cdot \frac{\partial X}{\partial S^{α}}) .

The vectors $\partial N / \partial S^{α}$ are defined from the derivatives of the interpolation functions and the “normals” at the nodes. These nodal normals are calculated as average values of the normals to the surfaces of all elements abutting the node. Abaqus determines if the surface is intended to be smooth at the node (the criterion is that the angle between the normals at the node should be less than 20°). If the surface is not calculated as smooth, separate normals are set up in the different surface branches at the node. Thus, $B_{α β}$ should be a reasonable approximation to the second fundamental form of the original reference surface.

Displacements

The nodal variables for shell elements are the displacements of the shell's reference surface, $u = x - X$ , and the normal direction, $n$ . Since $n$ is defined to be a unit vector, only two independent values are needed to define $n$ , so that this type of shell element needs only five degrees of freedom per node. In Abaqus this issue is addressed in two ways. At nodes in a smooth shell surface in those elements that naturally have five degrees of freedom per node, Abaqus stores the values of the projections of the change in $n$ projected onto two orthogonal directions in the shell surface at the start of the increment to define $n$ . Otherwise, Abaqus stores the usual rotation triplet, $ω$ , at the node. This latter method leaves a redundant degree of freedom if the node is on a smooth surface. A small stiffness is introduced locally at the node to constrain this extra degree of freedom to a measure of the same rotation of the shell's reference surface.

Interpolation

The same bipolynomial interpolation functions are used for all components of $u$ , $X$ , $N$ , and $n$ . The shear flexible shell elements in the library use bilinear interpolation (four nodes), fully biquadratic interpolation (nine nodes), and “serendipity” quadratics (eight nodes).

Strains

The reference surface membrane strains are

ϵ_{α β} = \frac{1}{2} (g_{α β} - G_{α β}) .

The curvature change is

κ_{α β} = B_{α β} - b_{α β} + \frac{1}{2} (B_{α}^{γ} ϵ_{γ β} + B_{β}^{γ} ϵ_{γ α}) .

The transverse shears are

γ_{3 α} = n \cdot t_{α},

where

t_{α} = \frac{\partial x}{\partial S^{α}} ∕ \sqrt{\frac{\partial x}{\partial S^{α}} \cdot \frac{\partial x}{\partial S^{α}}} (no sum on α)

is a unit vector, tangent to the $d S^{α}$ line in the current surface.

In addition to these strains, when six degrees of freedom are used at the nodes of the elements, the extra rotation degree of freedom is constrained with a penalty, as follows.

When such a node is the corner node of an element, define $T_{1}$ , $T_{2}$ , $N_{1}$ , $d S^{1}$ , and $d S^{2}$ in the element as above. Notice that these will be different in each element at the node, since the interpolated surface is not generally continuous. Then the strain to be penalized is defined as

γ_{S R C} = \frac{1}{2} (t_{1} \cdot {\bar{t}}_{2} - t_{2} \cdot {\bar{t}}_{1}),

where

{\bar{t}}_{α} = C \cdot T_{α}

is the rotated tangent direction, as defined by the rotation values at the node, and

t_{α} = \frac{\partial x}{\partial S^{α}} / \sqrt{\frac{\partial x}{\partial S^{α}} \cdot \frac{\partial x}{\partial S^{α}}} (no sum on α)

is the rotated tangent direction defined by the motion of the interpolated reference surface at the node.

At each midside node in the original configuration, define $N$ as the average surface normal for the elements of this surface branch at the nodes (there will be at most two such elements) and $T$ as the tangent to the edge. Then define

\bar{t} = C \cdot T and n = C \cdot N

as rotated values of $T$ and $N$ , as defined by the rotation values at the node. The vector

p = \bar{t} \times n

is then normal to $n$ and to the edge.

The strain to be penalized at these midside nodes is then defined as

γ_{S R M} = t \cdot p,

where

t = \frac{\partial x}{\partial S} / \sqrt{\frac{\partial x}{\partial S} \cdot \frac{\partial x}{\partial S}}

is the tangent to the edge of the element in the current position of the reference surface.

Penalties

The transverse shear strains are calculated at a set of reduced integration points and have the following stiffness associated with them:

K_{3 α} = G_{3 α} h Δ (area) / (1 + q Δ (area) / h^{2}),

where the $G_{3 α}$ are the elastic moduli associated with transverse shear. The $G_{3 α}$ are defined directly by the user or are computed from the elastic moduli given for the layers of the shell. h is the shell thickness; $Δ (area)$ is the value of reference surface area associated with this integration point in the numerical integration scheme; q is a numerical factor, currently set to $1 / 4 \times 10^{- 4}$ . (See Hughes et al., 1977, for a discussion of such factors.) Transverse shears are always treated elastically: nonlinear material calculations in shells are based on plane stress theory, using the membrane and bending strains to define the strain on the surface parallel to the shell's reference surface at each integration point through the shell's thickness.

When rotation constraints are required at nodes that use six degrees of freedom, the penalty used is

K = k G h Δ (area) / (1 + q Δ (area) / h^{2}) .

This is the same as the transverse shear constraint, except that $Δ (area)$ is here an area “assigned” to the node and the factor k is introduced. This (small) factor has been chosen based on numerical experiments, to be large enough to avoid singularities yet small enough to avoid adding significantly to the stiffness of the model.

These strain measures, with the interpolation specified above, give zero strain for any general rigid body motion

\begin{matrix} x & = X + u_{1} + (C_{1} - I) \cdot (X - X_{1}) \\ n & = C_{1} \cdot N, \end{matrix}

where $u_{1}$ , $C_{1}$ , and $X_{1}$ are constant.

First variations of strain

The first variations of the strains are

\begin{matrix} δ ϵ_{α β} & = \frac{1}{2} δ g_{α β} \\ δ κ_{α β} & = - δ b_{α β} + \frac{1}{2} (B_{α}^{γ} δ ϵ_{γ β} + B_{β}^{γ} δ ϵ_{γ α}) \\ δ γ_{3 α} & = δ n \cdot t_{α} + n \cdot δ t_{α} \\ δ γ_{S R C} & = \frac{1}{2} (δ t_{1} \cdot {\bar{t}}_{2} - δ t_{2} \cdot {\bar{t}}_{1} + t_{1} \cdot δ {\bar{t}}_{2} - t_{2} \cdot δ {\bar{t}}_{1}) \\ δ γ_{S R M} & = δ {\bar{t}}_{1} \cdot p + δ p \cdot \bar{t}, \end{matrix}

where

\begin{matrix} δ g_{α β} & = \frac{\partial δ u}{\partial S^{α}} \cdot \frac{\partial x}{\partial S^{β}} + \frac{\partial x}{\partial S^{α}} \cdot \frac{\partial δ u}{\partial S^{β}} \\ δ b_{α β} & = - \frac{1}{2} (\frac{\partial δ n}{\partial S^{α}} \cdot \frac{\partial x}{\partial S^{β}} + \frac{\partial δ n}{\partial S^{β}} \cdot \frac{\partial x}{\partial S^{α}} + \frac{\partial n}{S^{α}} \frac{\partial δ u}{\partial S^{β}} + \frac{\partial n}{\partial S^{β}} \cdot \frac{\partial δ u}{\partial S^{α}}) \\ δ n & = δ ω \times n \\ δ {\bar{t}}_{α} & = δ ω \times {\bar{t}}_{α} \\ δ t_{α} & = {(\frac{\partial x}{\partial S^{α}} \cdot \frac{\partial x}{\partial S^{α}})}^{- \frac{1}{2}} [I - t_{α} t_{α}] \cdot \frac{\partial δ u}{\partial S^{α}} (no sum on α) \end{matrix}

and at the midside nodes

δ p = δ ω \times p .

Second variations of strains

In forming the initial stress matrix we approximate by neglecting $d δ n$ , $d δ t$ , etc, to simplify the expressions and reduce the cost of forming the matrix. Numerical experiments have suggested that, at least for the problems tested, this does not significantly affect the convergence rate. With this approximation,

d δ ϵ_{α β} = \frac{1}{2} (\frac{\partial δ u}{\partial S^{α}} \cdot \frac{\partial d u}{\partial S^{β}} + \frac{\partial δ u}{\partial S^{β}} \cdot \frac{\partial d u}{\partial S^{α}})

\begin{matrix} d δ κ_{α β} = & \frac{1}{2} (\frac{\partial ω}{\partial S^{α}} \times n \cdot \frac{\partial d u}{\partial S^{β}} + δ ω \times \frac{\partial n}{\partial S^{α}} \cdot \frac{\partial d u}{\partial S^{β}} \\ + \frac{\partial ω}{\partial S^{β}} \times n \cdot \frac{\partial d u}{\partial S^{α}} + δ ω \times \frac{\partial n}{\partial S^{β}} \cdot \frac{\partial d u}{\partial S^{α}} \\ + \frac{\partial ω}{\partial S^{α}} \times n \cdot \frac{\partial δ u}{\partial S^{β}} + d ω \times \frac{\partial n}{\partial S^{α}} \cdot \frac{\partial δ u}{\partial S^{β}} \\ + (\frac{\partial ω}{\partial S^{β}} \times n \cdot \frac{\partial δ u}{\partial S^{α}} + d ω \times \frac{\partial n}{\partial S^{β}} \cdot \frac{\partial u}{\partial S^{α}}) \\ + \frac{1}{2} (B_{α}^{γ} d δ ϵ_{γ β} + B_{β}^{γ} d δ ϵ_{γ α}) \end{matrix}

\begin{matrix} d γ_{3 α} = & g_{α}^{- \frac{1}{2}} δ ω \times n \cdot (I - t_{α} t_{α}) \cdot \frac{\partial d u}{\partial S^{α}} \\ + g_{α}^{- \frac{1}{2}} d ω \times n \cdot (I - t_{α} t_{α}) \cdot \frac{\partial u}{\partial S^{α}} (no sum on α) \end{matrix}

\begin{matrix} d δ γ_{S R C} = & g_{1}^{- \frac{1}{2}} δ ω \times {\bar{t}}_{1} \cdot (I - t_{2} t_{2}) \cdot \frac{\partial d u}{\partial S^{2}} \\ - g_{2}^{- \frac{1}{2}} δ ω \times {\bar{t}}_{2} \cdot (I - t_{1} t_{1}) \cdot \frac{\partial d u}{\partial S^{1}} \\ + g_{1}^{- \frac{1}{2}} d ω \times {\bar{t}}_{1} \cdot (I - t_{2} t_{2}) \cdot \frac{\partial δ u}{\partial S^{2}} \\ - g_{2}^{- \frac{1}{2}} d ω \times {\bar{t}}_{2} \cdot (I - t_{1} t_{1}) \cdot \frac{\partial δ u}{\partial S^{1}} \end{matrix}

and

\begin{matrix} d δ γ_{S R M} = & g^{- \frac{1}{2}} d ω \times p \cdot (I - t t) \cdot \frac{\partial δ u}{\partial S^{2}} \\ + g^{- \frac{1}{2}} δ ω \times p \cdot (I - t t) \cdot \frac{\partial d u}{\partial S^{1}} . \end{matrix}

Internal virtual work rate

For these shell elements the internal virtual work rate is assumed to be

\begin{matrix} δ W^{I} & = \int_{A} \int_{h} σ^{α β} δ ε_{α β}^{f} d z d A \\ + \sum_{r} K_{I}^{(r)} γ_{3 α}^{(r)} δ γ_{3 α}^{(r)} \\ + \sum_{n^{c}} K_{I I}^{(n)} γ_{S R C}^{(n)} δ γ_{S R C}^{(n)} \\ + \sum_{n^{m}} K_{I I I}^{(n)} γ_{S R M}^{(n)} δ γ_{S R M}^{(n)}, \end{matrix}

where $K_{I}^{(r)}$ , $K_{I I}^{(n)}$ , and $K_{I I I}^{(n)}$ are the transverse shear stiffness and the penalties defined above and r indicates the integration points at which transverse shears are calculated, $n^{c}$ indicates corner nodes at which six degrees of freedom are used, and $n^{m}$ indicates midside nodes at which six degrees of freedom are used. Here $ε_{α β}^{f}$ and $σ^{α β}$ are the strain and stress in the ( $d S^{α}$ , $d S^{β}$ ) material directions in a surface offset by a distance z from the reference surface. The usual Kirchhoff assumption is adopted:

ε_{α β}^{f} = ϵ_{α β} + z κ_{α β},

so that the first term above is

\int_{A} (δ ϵ_{α β} \int_{h} σ^{α β} d z + δ κ_{α β} \int_{h} z σ^{α β} d z) d A .

The thickness direction integrations are performed numerically in Abaqus. The integration scheme is a Simpson's rule, of user-chosen order. The shell can also be considered layered, with different properties at each layer and a different integration scheme assigned (by the user) to each layer.

Pressure load stiffness

The load stiffness associated with pressure loading is often important in shells, especially in eigenvalue buckling estimates on elastic shells. In Abaqus/Standard the pressure load stiffness is implemented as a symmetric form, thus assuming that the pressure magnitude is constant over the surface and neglecting free edge effects. See Hibbitt (1979) and Mang (1980) for details.

The load stiffness is obtained in such a form as follows. The external virtual work associated with pressure is

δ W^{e} = \int_{A} p \cdot δ u d A,

where $p$ is the pressure load per unit area, given in terms of the (externally prescribed) pressure magnitude, p, as

p d A = p \frac{\partial x}{\partial θ^{1}} \times \frac{\partial x}{\partial θ^{2}} d θ^{1} d θ^{2} .

Thus,

δ W^{e} = \int_{A} p (\frac{\partial x}{\partial θ^{1}} \times \frac{\partial x}{\partial θ^{1}}) \cdot δ u d θ^{1} d θ^{2} .

The change in this term caused by change of displacement of the shell (the “load stiffness”) is

d δ W^{e} = \int_{A} p δ u \cdot (\frac{\partial x}{\partial θ^{1}} \times \frac{\partial d u}{\partial θ^{2}} - \frac{\partial x}{\partial θ^{2}} \times \frac{\partial d u}{\partial θ^{1}}) d θ^{1} d θ^{2},

since we assume that pressure magnitude, p, is externally prescribed and has no dependence on position, $x$ . Neglecting free edge effects, and assuming the magnitude p is uniform, results in the symmetric form

\begin{matrix} d δ W^{e} & = \int_{A} \frac{1}{2} p [\frac{\partial x}{\partial θ^{1}} \cdot (\frac{\partial d u}{\partial θ^{2}} \times δ u + \frac{\partial δ u}{\partial θ^{2}} \times d u) \\ - \frac{\partial x}{\partial θ^{2}} \cdot (\frac{\partial d u}{\partial θ^{1}} \times δ u + \frac{\partial δ u}{\partial θ^{1}} \times d u)] d θ^{1} d θ^{2} . \end{matrix}

This is the pressure load stiffness provided in Abaqus.